Introduction
In this project, we explore different ways of using frequencies to process and combine images interestingly. For example, similar to our phones, we can sharpen images by emphasizing high frequencies. We can also extract edges using finite difference operators. Hybrid images that look one way close up and another far away can also be created by combining the high frequencies of one image with the low frequencies of another. Lastly, images can be blended at various frequencies with the help of Gaussian and Laplacian stacks.
Fun with Filters
Finite Difference Operator
Finite Difference Operators help detect edges by highlighting regions where pixel intensity changes rapidly, which usually corresponds to edges or boundaries in the image. In two-dimensional images, the finite difference operator computes the derivative in horizontal (x) and vertical (y) directions. These derivatives are calculated using simple convolution filters, such as:
- Dx = [1, -1]: for detecting horizontal changes (vertical edges).
- Dy = [[1], [-1]]: for detecting vertical changes (horizontal edges).
When these operators are applied to an image, they produce two gradient images:
- The gradient in the x-direction highlights vertical edges.
- The gradient in the y-direction highlights horizontal edges.
By combining these gradients, we can produce an edge-detection image that reveals significant changes in intensity.
Results





Derivative of Gaussian (DoG) Filter
Blurred Finite Difference
A Gaussian filter is applied to the image to reduce noise and small details. I used a kernel of size 5 with sigma = 1 created using cv2.getGaussianKernel. I created a blurred version of the original image by convolving with the Gaussian and repeating the procedure in the previous part.
There are some very noticeable differences between the two methods. The binarized edges are much thicker and more prominent than before. Furthermore, some of the unnecessary details Details near the bottom of the pictures have been removed, and the fine details from the camera have also been removed.





Derivative of Gaussian (DoG)
Another method is to do the same thing with a single convolution instead of two by creating a derivative of Gaussian filters. the Gaussian kernels used to blur the image are instead convolved beforehand using the dx and dy kernels to produce dx_gaussian and dy_gaussian. We then convolute the original image with the new filters.





Comparison


As can be seen, the two images are identical, apart from a few slight differences in length and shape of minor edges.
Hybrid Images
Approach
This part of the assignment aims to create hybrid images. Hybrid images change in interpretation based on the viewing distance. This is based on the idea that high frequency tends to dominate when the viewing distance is closer, but at a distance, only the low-frequency part of the signal can be seen. Blending the high-frequency portion of one image with the low-frequency portion of another gives you a hybrid image that leads to different interpretations at different distances. For a low-pass filter, I used a standard 2D Gaussian filter. I used the original image minus the low frequencies for a high-pass filter. Since both images are different, they require different kernel sizes and sigmas for the Gaussians.
Derek + Cat
For the Dererk Cat hybrid image, I used a sigma of 5 and a kernel size of 10 for Derek. I used a sigma of 15 for the cat and a kernel size 13. From a close-up, we can see that the cat's features dominate the picture. However, as we go back, we can only see Derek properly.



Starry Night + Mountain Landscape (My Favorite)
For the Starry Night Mountain hybrid image, I chose to use a sigma of 2 and kernel size of 10 for the Mountain Landscape. For the Starry Night painting I chose to use a sigma of 10 and kernel size of 13. As can be seen below, from close up we can see the starry night painting dominate the picture. However, as we go further back we see the mountain landscape dominate.


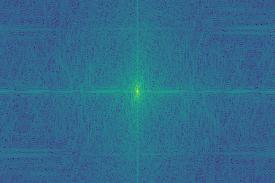
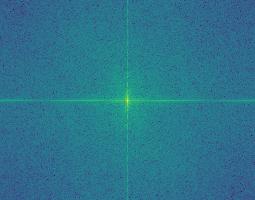
Fourier Transforms for Starry Night + Mountain Landscape

Smily/Sad Face (Failure)
For the Smily/Sad Face hybrid image, I chose to use a sigma of 2 and kernel size of 10 for the smily face. For the sad face I chose to use a sigma of 8 and kernel size of 13. However, in this case it seems like there is no "Hybrid" effect. The sad face and smily face both seem to appear at all distances. This might be because the smily face is natively gray.



Gaussian and Laplacian Stacks
Approach
In this section, we create Gaussian and Laplacian Stacks of Images. These are very similar to the pyramids, except instead of downsampling, the previous level is blurred using a Gaussian kernel to make the next level. Furthermore, the Laplacian stack is calculated by laplacian_stack[i] = gaussian_stack[i] - gaussian_stack[i+1].
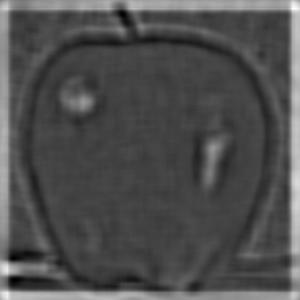
Apple
Gaussian Stack






Laplacian Stack

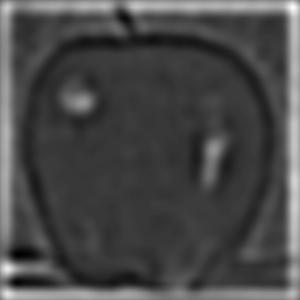
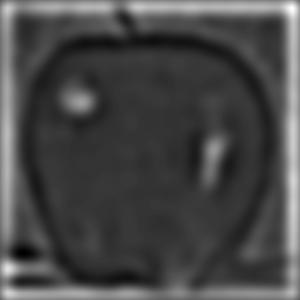


Orange
Gaussian Stack






Laplacian Stack

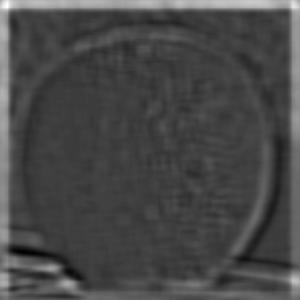
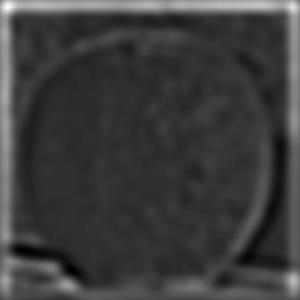
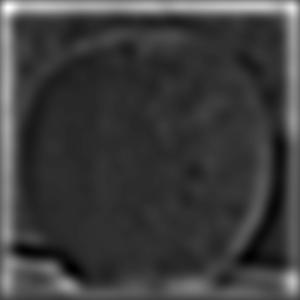
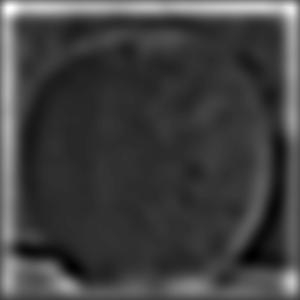

Multiresolution Blending
Approach
We can blend two images using the Gaussian and Lapacian stacks from above. The input images left and right are used to generate Laplacian stacks left_l_stack and right_l_stack using the method above. A Gaussian stack mask_g_stack is generated from the mask input image. To blend the images, for each level i in all three stacks, blended_laplacian_stack[i] = mask_gaussian_stack[i] * left_laplacian_stack[i] + (1 - mask_gaussian_stack[i]) * right_laplacian_stack[i].
Oraple




Tomaya (Tom Cruise + Zendaya)




Red Forest Through a Window




Laplacians of the 3
























