Introduction

In this project I implement and deploy diffusion models for image generation. It is divided into two parts. In part A, I use Stability AI's DeepFloyd Model implement diffusion sampling loops, and use them for other tasks such as inpainting and creating optical illusions. In part B, I implement a UNet Models from Scratch.

Part A: The Power of Diffusion Models!

Diffusion Model: Forward Process

The forward process gradually adds noise to a clean image \(x_0\), resulting in a noisy image \(x_t\).

Original Image (x₀)

Noisy Images at Different Timesteps

Classical Denoising

In this section, we apply classical Gaussian blur filtering to the noisy images generated in the forward process. Gaussian blur is a simple denoising technique that removes high-frequency noise.

Noisy Images at Different Timesteps

Gaussian Blur Denoising at Different Timesteps

One Step Denoising

In this section, we use a pretrained diffusion model to denoise noisy images generated in the forward process. The pretrained UNet model is conditioned on Gaussian noise levels, allowing it to estimate and remove noise from noisy images at different timesteps.

Additionally, this model is text-conditioned, so we pass a text prompt "a high quality photo" to help guide the denoising process. This prompt embedding provides additional context to the UNet.

Noisy Images at Different Timesteps

One Step Denoising at Different Timesteps

Iterative Denoising

In the previous section, we used a pretrained UNet to perform one-step denoising. However, diffusion models are designed for iterative denoising, progressively refining noisy images until we obtain an estimate of the original clean image \(x_0\).

Instead of performing 1000 steps (which is computationally expensive), we use a technique called strided timesteps to skip steps and speed up the process. By choosing a regular stride (e.g., 30), we reduce the number of timesteps while maintaining denoising quality.

Noisy to Clean Image Transition

Below, we show the iterative denoising process using strided timesteps (\(t = 690, 540, 390, 240, 90\)):

Predicted Clean Images

Diffusion Model Sampling

In this section, we use the diffusion model to generate images from random noise. By starting at \(i_{\text{start}} = 0\), we begin the denoising process with pure noise and iterate until the final clean image is obtained. This effectively allows the model to create new images from scratch.

For this example, we use the text prompt "a high quality photo" to guide the image generation. Below are 5 samples generated by the model:

Classifier-Free Guidance (CFG)

Classifier-Free Guidance (CFG) is a technique that enhances image quality by balancing conditional and unconditional noise estimates. In CFG, we compute both a noise estimate conditioned on a text prompt (\( \epsilon_c \)) and an unconditional noise estimate (\( \epsilon_u \)). The final noise estimate is given by:

Here, \( \gamma \) controls the strength of the guidance. When \( \gamma = 0 \), we use the unconditional noise estimate, and when \( \gamma = 1 \), we fully condition on the text prompt. For \( \gamma > 1 \), we achieve higher-quality images by amplifying the guidance signal. For more details, refer to this blog post.

Generated Images

Below are 5 images generated using CFG with \( \gamma = 7 \):

Image-to-Image Translation

Image-to-image translation involves taking an existing image, adding controlled amounts of noise to it, and using a diffusion model to denoise it back into the natural image manifold. This process allows us to make creative "edits" to the original image, where the degree of noise determines the extent of the edits.

Editing Hand-Drawn and Web Images

This procedure is particularly effective when applied to non-realistic images, such as hand-drawn sketches, paintings, or abstract scribbles. By applying diffusion models, we can project these images onto the natural image manifold, resulting in creative transformations. Below, we experiment with various hand-drawn and web images, running them through iterative denoising processes to see how they evolve into realistic outputs.

Inpainting

Inpainting involves restoring or editing specific parts of an image while preserving the rest. This method is inspired by the RePaint paper, which utilizes diffusion models to fill in missing or altered parts of an image.

Formula

At each timestep t, we update the image as follows:

            x_t = m * x_t + (1 - m) * forward(x_orig, t)
            

Text-Conditioned Image-to-Image Translation

In this section, we will perform the same image-to-image translation as the previous step, but now we will guide the translation using a text prompt. Instead of simply projecting the image onto the natural image manifold, we introduce text-based control, allowing the model to generate results aligned with specific language-based instructions.

Visual Anagrams

In this section, we create Visual Anagrams using diffusion models to generate optical illusions. The goal is to create an image that resembles one thing when viewed normally, but transforms into another when flipped upside down.

Hybrid Images

In this section, we create Hybrid Images using a technique called Factorized Diffusion. Hybrid images are created by blending low and high-frequency components derived from two separate noise estimates using diffusion models. To create a composite image, we combine the low frequencies from one noise estimate with the high frequencies of another. The resulting hybrid image shows different characteristics depending on the viewing distance.

Training a Single-Step Denoising UNet

The Single-Step Denoising UNet is designed to denoise a noisy image (z), approximating the clean image (x). The process combines a specialized architecture (the UNet) and a noise-injection process for training. Here's an overview:

Forward Process (Generating Training Data)

To train the denoiser, we simulate noisy data by adding noise to clean images (x):

Here:

• σ is the noise level, and we vary it across a range (e.g., σ = [0.0, 0.2, 0.4, ...]).
• This process creates pairs (z, x), where z is the noisy input, and x is the target.

Training the UNet

The training objective is to minimize the reconstruction loss between the predicted clean image (hat{x}) and the ground truth (x):

Key Steps:

• Input: The noisy image z and its corresponding clean image x.
• Prediction: The UNet outputs hat{x} = D_θ(z), an estimate of the clean image.
• Loss: The L2 loss measures the difference between hat{x} and x.
• Optimization: Gradients are backpropagated to update the UNet's parameters.

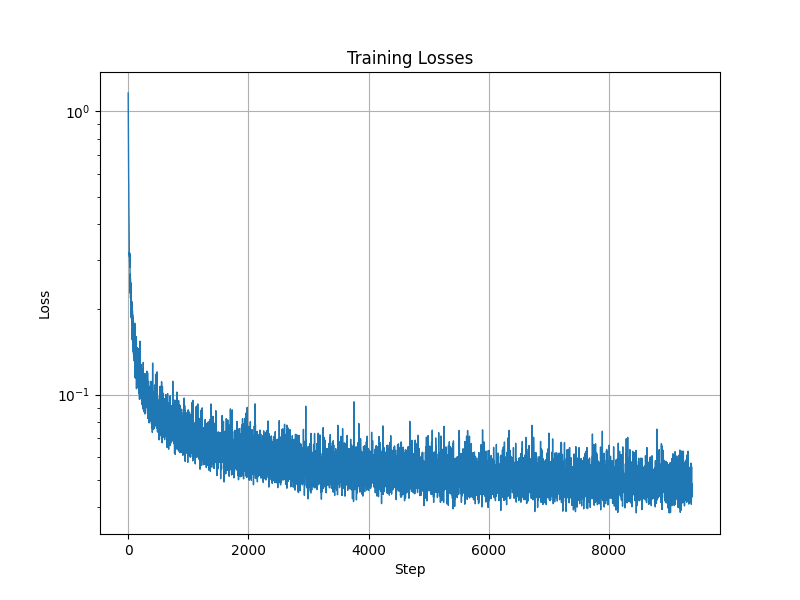
High-Level Overview of the Time-Conditioned UNet

The Time-Conditioned UNet is an enhancement of the Single-Step Denoising UNet, designed to model the diffusion process iteratively across timesteps. This model is essential in diffusion models, where denoising at each timestep depends on both the input and the timestep itself. Here's an overview:

Forward Process (Training Data Generation)

To train the model, we simulate noisy images at various timesteps using the forward diffusion process:

Here:

• x_0: Clean image.
• x_t: Noisy image at timestep t.
• α̅_t: Cumulative product of noise scheduling terms.
• ε: Gaussian noise.

This process creates pairs (x_t, t) where the model learns to predict ε.

Training the Time-Conditioned UNet

The objective of training is to minimize the error in predicting the noise term ε:

Key Steps:

• Input: Noisy image x_t and its timestep t.
• Output: The UNet predicts ε_θ(x_t, t), the noise added to x_0 at timestep t.
• Loss: L2 loss measures the difference between the predicted and actual noise.
• Optimization: Backpropagation updates the UNet's parameters.

Iterative Denoising (Inference)

During inference, the Time-Conditioned UNet performs iterative denoising starting from pure noise (x_T) and progressing toward the clean image (x_0):

Here:

• z: Gaussian noise added for intermediate steps.
• This formula ensures that the image is gradually denoised step-by-step.

Summary

The Time-Conditioned UNet builds on the standard UNet by conditioning on timesteps, making it suitable for iterative denoising tasks. Its strengths include:

• Timestep Adaptation: Learns to predict noise specific to each timestep.
• Iterative Denoising: Gradually refines the noisy image to reconstruct the clean image.
• Generalization: Trained on varying noise levels, enabling robustness across timesteps.

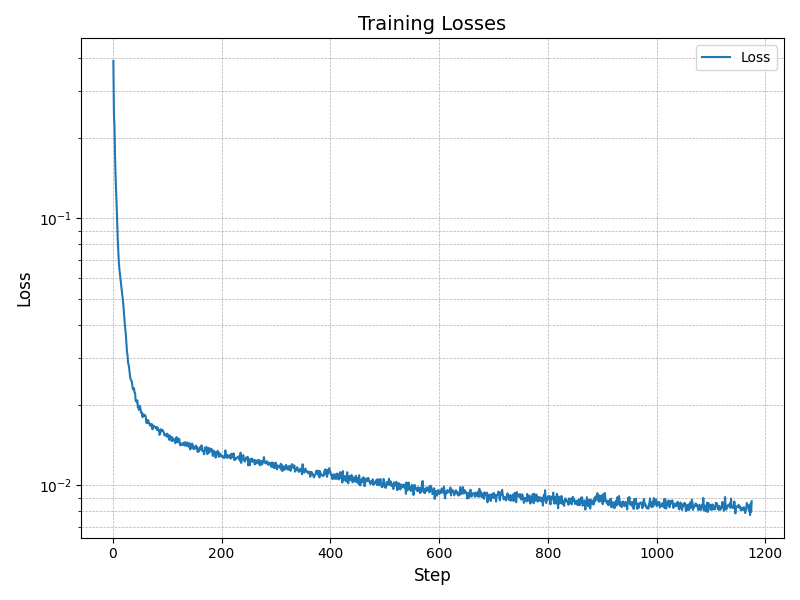
High-Level Overview of the Class-Conditioned UNet

The Class-Conditioned UNet builds on the foundation of the Time-Conditioned UNet by introducing an additional conditioning mechanism based on image class labels. This model is designed to denoise images while incorporating semantic information about the image class, making it suitable for class-conditional diffusion models. Here's an overview:

Forward Process (Training Data Generation)

To train the model, we simulate noisy images at various timesteps using the forward diffusion process:

Here:

• x_0: Clean image.
• x_t: Noisy image at timestep t.
• α̅_t: Cumulative product of noise scheduling terms.
• ε: Gaussian noise.

This process creates pairs (x_t, t, c), where c is the class label, and the model learns to predict ε.

Training the Class-Conditioned UNet

The objective of training is to minimize the error in predicting the noise term ε:

Key Steps:

• Input: Noisy image x_t, its timestep t, and class label c.
• Output: The UNet predicts ε_θ(x_t, t, c), the noise added to x_0 at timestep t for class c.
• Loss: L2 loss measures the difference between the predicted and actual noise.
• Optimization: Backpropagation updates the UNet's parameters.

Classifier-Free Guidance (CFG)

During inference, the Class-Conditioned UNet can leverage Classifier-Free Guidance (CFG) to balance fidelity and diversity:

Here:

• ε_u: Unconditional noise estimate (no class conditioning).
• ε_c: Class-conditional noise estimate.
• γ: CFG scale that controls the strength of class conditioning.

Iterative Denoising (Inference)

During inference, the Class-Conditioned UNet performs iterative denoising starting from pure noise (x_T) and progressing toward the clean image (x_0):

Here:

• z: Gaussian noise added for intermediate steps.
• This formula ensures that the image is gradually denoised step-by-step while adhering to the specified class.

Summary

The Class-Conditioned UNet builds on the Time-Conditioned UNet by incorporating class-conditioning, making it capable of generating or denoising images conditioned on a specific class. Its strengths include:

• Class Awareness: Learns to predict noise specific to each class label.
• Timestep Adaptation: Adapts denoising to the current timestep.
• Versatility: Suitable for class-conditional image generation and denoising tasks.